反三角函数导数推导过程，反三角函数导数推导过程不需要考虑定义域吗

投稿用户 • 2022年9月22日 pm11:13 • 范文大全 • 阅读 611

在数学史的浩瀚星空里遨游，在高等数学的神奇世界里忘记自我??????

有大学同学前段时间问我为什么每天朋友圈里讲授的都是高中范围内的数理知识，但你经常恶补和研读很多大学的高等数学的相关课程呢？

我个人认为：一切不以“高等数学为目标的”数学研究都是“耍流氓”。那样只会落得个“杂耍数学家”或“数学骗子”的称号。

近期看到相关报道，取得辉煌成就今年刚刚回国办学的数学家丘成桐，在接受采访中，直指中国数学和自然科学教育的弊端：那就是只会做题，而不擅长思考；只强调熟练运用固定模型，而忽略数学本质。丘成桐也说过：如果一个学生对“微积分”不感兴趣，那么即使他高考或奥赛成绩再好，也不会在数学研究的路上走得太远。

回顾整个数学发展史就会发现，现在我们熟知的初高中各种数学知识，其实充其量只能称作“古典数学”或“初级数学”。一个学生在初中或高中即使数学学得再好，也没有什么值得过度骄傲的，因为这都是一两千年之前古代数学家们的研究成果，里面体现的数学理论和解题思路也是我之前说的：在宏观、静态、线性条件下的简单独立模型而已。

因为通过长时间钻研数学发展史和相关数学典籍（无论初高中教材或者课外读物），我发现从小学到高考，从一般小测到高中数学奥赛，用到的代数学理论和几何模型中，大约90％以上都是至少1000多年以前的数学知识。

本人觉得普通数学到高等数学或近代数学的分割点应该是17世纪中间的几十年。1640年左右笛卡尔完善了解析几何，而在1665-1666年牛顿和莱布尼茨先后创立“微积分”理论。这两个事件吹响了初等数学向高等数学跨越的号角。说句题外话，那时的中国，刚刚进入康熙年间，继位不到四年的“小玄烨”外攘“反清复明”的前朝旧部，内斗权倾朝野的“强敌”鳌拜。当这个东方文明古国还在“四书五经”的对仗押韵里自我陶醉的时候，欧洲众国已冲破中世纪黑暗，正向着人类自然科学的最前沿迈进。

而学数学就跟做人的道理是一样的，如果让我选两句关于学数学或做人的名言警句，那我第一会选“温故而知新”；第二会选“千淘万漉虽辛苦，吹尽狂沙始到金”。只有最大限度地汲取前人的知识营养，才能不断地获取新的知识；而近现代数学出现的数不胜数的数学分支和公式定理，都是数学家凭借超强的演算能力和竭尽毕生心血的付出得来的，比如牛顿、笛卡尔、泰勒、拉格朗日等等，都是在大量枯燥繁琐的多项式或方程函数计算里，将那些“金子般”的结论淘洗了出来。

在高等数学里，“微积分”永远是独享“主角光环”的。在数学家天马行空的想象力下，各种函数的求导和积分公式，配合着初等数学的运算技巧，催生了一个又一个揭示微观世界和非线性变化场景的定理结论。而现在大学理工科学生接触最多的莫过于各种级数、展开式以及相关变换。

以我最最佩服的泰勒展开式为例，学生只要将十几个特殊函数的泰勒公式牢牢背过就能做题了（而且用这些公式做一些比较难的高考选择填空题会更加方便，比如今年高考新一卷那道最难的同构导函数比较大小的选择题）。

但是如果想深入地感受泰勒级数的魅力，就必须了解泰勒他们在摸索一般函数变为“等价n次多项式”时的“无中生有”的思路。真可谓“神来之笔”，让人赞叹不绝！

他们从一些比较常见的函数如sinx、e的x次方、lnx、分式函数、反三角函数等n次求导后，突发奇想地猜测：“会不会有一个统一的方法和模型，让几乎所有的能写出来的函数，都表示为一个带有n阶求导的n次多项式呢？”于是以泰勒为代表的数学家们首开先河，通过严谨的计算，终于推导出了函数的级数展开形式的“雏形”，第一次用微积分和多项式运算等知识触摸到了函数等价转化的本质。

后来在他的成果的推动下，出现了一系列的函数展开式，为推动复杂函数求值、函数动态分析、计算科学、信号学等等做出了巨大的贡献。

可以说没有函数理论、没有微积分、没有无穷级数和泰勒展开式，就没有之后的傅立叶变换等思想，也没有信号学和通信领域的蓬勃发展，更没有我们“赖以生存”的移动互联时代。

感慨之余，只能羡慕嫉妒牛顿、泰勒、拉格朗日等数学家的“绝世才华”。

最后，希望这篇深夜写就的“高等数学入门级”科普文章，能够鼓舞那些正被高中数学物理压得喘不过气来的“小朋友”，和刚刚迈入大一正与高等数学亲密接触的“大朋友”们，希望你们都能熬过这最最宝贵的学习阶段，早日悟得数学的真谛，为国家的繁荣和人类科技文明的飞跃做出最大的贡献，实现人生的终极价值！晚安！！

............试读结束............

查阅全文加微信：3231169

如来写作网：gw.rulaixiezuo.com（可搜索其他更多资料）

本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容，请发送邮件至 3231169@qq.com 举报，一经查实，本站将立刻删除。
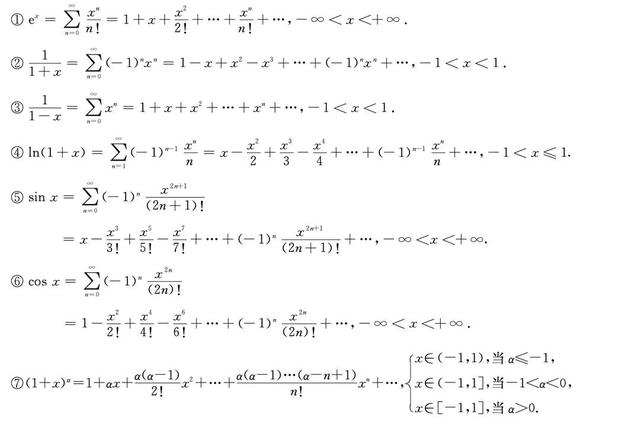
如若转载，请注明出处：https://www.haowenren.com/8190.html

反三角函数导数推导过程，反三角函数导数推导过程不需要考虑定义域吗

相关推荐